자료 출처: https://www.youtube.com/c/DdmixBlogspot/featured
Jake Lee
Digital Dynamics ~ http://ddmix.blogspot.com C++로 배우는 알고리즘, 스케치업 등의 동영상 강의를 싣고 있습니다.
www.youtube.com
소스 코드 링크: https://github.com/leejaku17/cppalgo_2002/blob/master/Week3/Search/RBTreeMap.h#L49

1. 부모 노드는 왼쪽 서브 트리 보다 크고 오른쪽 서브 트리보다 작다.
- 이진 검색 트리와 동일한 성질로, 탐색 과정에서 필수적으로 사용되는 개념
2. Root에서 Leaf로 가는 경로의 검정 노드의 수는 모두 같다.
- 유일하게 구현 단계에 원칙으로 작용하지 않는 RB 트리 본연의 성질. 올바른 알고리즘으로 기능들을 구현할 경우 자연스럽게 보장되는 성질이다.
3. 새로 삽입되는 노드는 Leaf에 위치하며 빨간 노드이다.
- 삽입 구현 단계에서의 중요 성질. Root부터 1번 성질을 기준으로 올바른 위치로 탐색해 내려가며, 상향 색변환을 진행하고, 위치에 맞는 NULL Leaf에 도달할 경우 삽입을 진행한다.
4. 경로상에 연이어 두개의 빨간 노드가 있을 수 없다.
- 삽입, 탐색등 상향, 하향 색변환을 진행 할 경우 연속된 빨간 노드가 생기게 되고 이 경우 적절한 회전을 통해 RB트리의 성질을 유지하며 변화 시킨다.
5. 부모의 두 자식 노드가 모두 빨간 노드이면, 부모를 빨간 노드로 하고, 자식은 검정 노드로 바꿀 수 있다. (vice versa)
- 상향 하향 색변환에 사용되는 성질.
6. Root 노드는 빨간 노드일 수 없다.
- 삭제, 회전 등을 진행 할 시 Root 노드가 바뀌게 되는데 이때 Root 노드는 반드시 검정 노드로 변환 시킨다.
7. 빨간 노드는 자식이 없던가, 있다면 두개의 검정 노드여야 한다.
- 2, 3, 4 트리의 성질을 이어받는 부분. 빨간 부모 노드가 존재한다면 234 트리의 경우 3노드나 4노드인데 이 경우 red black 노드로 분할 시 red가 항상 2개의 자식 노드를 가지고 분할 된다고 보면 된다.
8. 검정 노드는 자식이 없던가, 있다면 하나의 빨간 노드나 두개의 빨간 노드나, 두개의 검정 노드를 가진다.
- 단 하나의 검정 노드를 자식으로 가질 수 없다.
Red Black 트리

2, 3, 4 트리를 red black 트리로 변환한 모습. 7번 성질 설명.
2 - 3 - 4 트리의 원리와 성질
234트리란? 2노드, 3노드, 4노드가 있는 균형 탐색 트리
2 노드 : 한 개의 키와 두 개의 자식을 갖는 노드
3 노드 : 두 개의 키와 세 개의 자식을 갖는 노드
4 노드 : 세 개의 키와 네 개의 자식을 갖는 노드
#키 = 원소, 자식 = 아래로 연결된 노드

red - black 트리에서 성질을 유지한 체 할 수 있는 동작 두 가지.

상향식의 경우 삽입 알고리즘에 사용된다. 삽입 위치가 될 Leaf를 향해 Root 부터 탐색해 내려가며 상향 색변환을 실시한다. 상향 색변환 후 연속된 빨간 노드가 생긴다면 회전으로 해결한다.
(ex 오른쪽 그림에서 G가 빨간 노드 일때 B가 상향 색변환으로 빨강으로 변환하는 경우)

하향 색변환의 경우 삭제 알고리즘에서 사용된다.
주 역할은 삭제해야할 노드의 색을 빨강으로 바꾸기 위함이다.
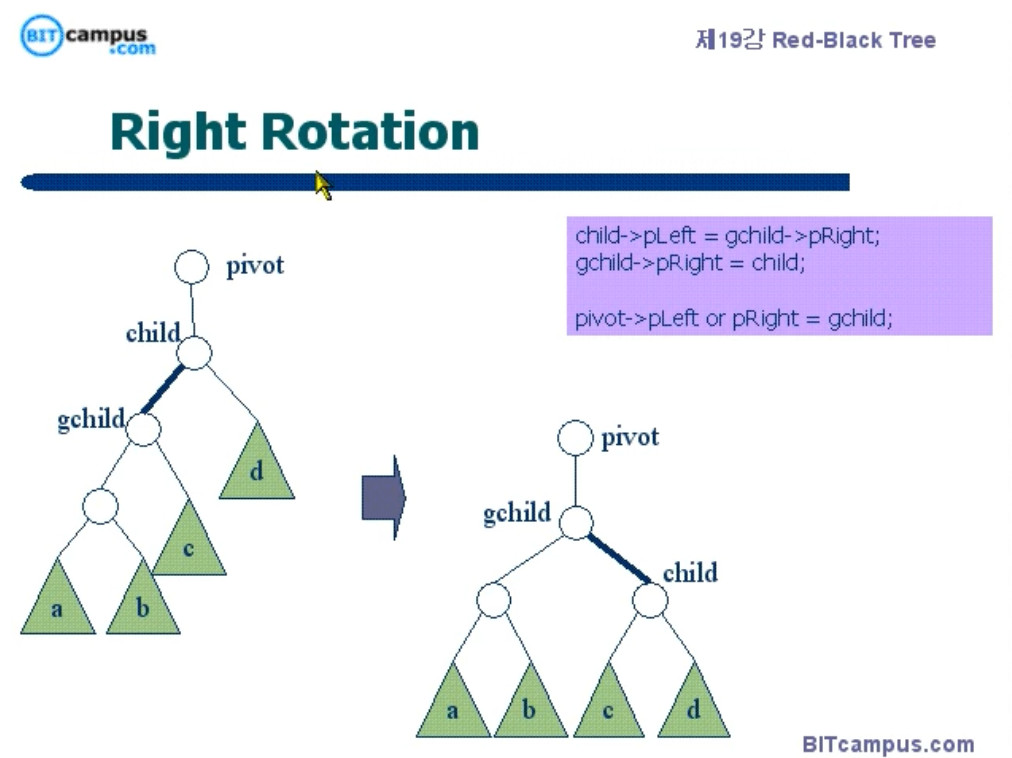

회전의 경우 구현에서 가장 중요한 점은 이 세 네 점이다.
pivot, child, gchild 아니면 순서대로 great grand parent, grand parent, parent, 빈노드 = child
회전 방향이 왼쪽인지 오른쪽인지는 pivot 노드의 값과 회전을 진행할 노드의 값과 비교해 알 수 있다.
Red Black Tree 삽입 알고리즘

Leaf에 도달할 시 leaf에 달려있는 Null leaf 중 적절한 위치에 삽입한다.
로직은 간단한데 , 하향 탐색을 진행하며 가능할 때마다 상향 색변환을 실시하고, 빨간 노드가 연속 될 경우 회전을 실시해 해결한다.


간단한 좌 우 회전
1. G노드 방문 -> 상향 색변환 가능하기에 실시.
2. E - G 빨간노드 연속, 회전 실시
3. G = tree, E = parent , C = great parent, A = pivot


rotation을 두번 진행해야하는 경우는 연속된 빨강 노드가 좌 우, 우 좌 식으로 이어졌을 경우다.
이를 판단하는 기준은 gp(C)와 p(G)가 될 수 있는데, (gp > G) != (p > E) 일 경우다.
반대로 회전이 한번만 필요할 경우는(gp > G) == (p > E) 다
이는 루트 기준 왼쪽이든 오른쪽이든 상관 없다. 둘다 틀리거나 둘다 맞다면 회전이 한번 필요하고 둘의 대소관계가 다르다면 회전이 두번 필요한 경우가 된다.
삭제 알고리즘

삭제 알고리즘은 삽입보다 복잡하다.
기본적으로 원칙 1: Leaf 3-4노드의 삭제는 Trivial, 즉 비교적 쉽기 때문에 이를 위해 원칙 2, 3이 사용되어 3-4노드로 만들어가며 진행한다.

1원칙에 해당하는 원소의 경우 위의 그림과 같이 쉽게 삭제 할 수 있다. (내부 노드 x)

del = 삭제하고자 하는 노드
delp = 부모
sib = 형제
del 노드의 부모를 빨강 노드로 바꾼다면 하향 색변환이 가능한 경우가 생기고 하향 색변환을 한다면 del 노드가 3-4노드로 바뀌게 된다.

형제와 결합하기는 하향 색변환이다.
형제, 삭제 노드의 자식 노드가 모두 검정 노드일 경우 가능

하향 색변환아 불가능한 경우 : 형제 노드의 자식 노드가 빨강 자식이 없어야 한다. ( RB트리 성질 참고)
이 경우 단일 회전 혹은 이중 회전을 진행해 삭제하려는 노드를 3-4노드로 바꿔 준다.

형제가 빨강 노드를 자식으로 가지고는 있는데 그게 꺽이는 위치라면, 이중 회전을 진행해야한다.

삭제하려는 노드가 내부 노드의 경우, 이 경우 D, D의 오른쪽 서브트리에서 가장 작은 값과 값을 바꿔 준다.
위가 가능한 이유는 오른쪽 서브트리의 가장 작은 값은 (여기선 E) D가 없을 경우, D의 위치에 있어도 RB트리의 성질을 모두 충족하기 때문.
그 후 아래 쪽의 E 노드를 삭제하는 문제로 바꾼다.
'sw사관학교 정글 2기 > 컴퓨터 시스템' 카테고리의 다른 글
| c - 비트 연산자, 매크로 (0) | 2021.09.10 |
|---|---|
| Malloc Lab - assignment (0) | 2021.09.09 |
| Red Black Tree - 소스 코드 해석- (1) | 2021.09.07 |
| 이진 탐색 트리 - binary search tree - 퍼옴 (0) | 2021.09.06 |
| C 포인터 (1) | 2021.09.02 |




댓글