좋은 설명 링크:
https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html
https://terms.naver.com/entry.naver?docId=3579618&cid=59086&categoryId=59093
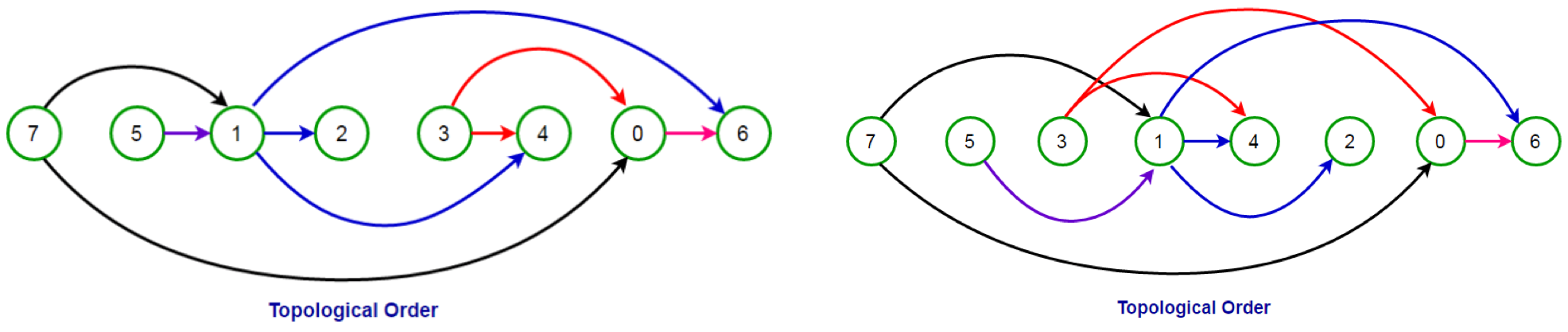
위상 정렬이란?
위상 정렬(topological sorting)은 유향 그래프의 꼭짓점들(vertex)을 변의 방향을 거스르지 않도록 나열하는 것을 의미한다.
개인적 노트
위상정렬이라는 알고리즘은 기본적으로 단순히 노드/꼭짓점들을 진입 방향에따라 순서대로 나열 할 뿐인 알고리즘이다. 위상정렬을 마친 답은 여러 종류가 있을 수 있고, 이를 응용하는게 알고리즘 문제들의 특징이다.
가장 기본적인 위상정렬을 시행하는 문제로 백준-줄세우기 가 있다.
from collections import deque
import sys
input = sys.stdin.readline
# 노드의 개수 / 간선 개수
# ex) N = 6 / M = 5
n, m = map(int, input().split())
# 앞 원소에서 뒷 원소를 향하는 간선들 / 진출 방향
# ex) routes = [[1, 2], [2, 3], [4, 3], [5, 3], [6, 5]]
routes = []
for _ in range(m):
a, b = map(int, input().split())
routes.append([a, b])
# 각 노드들이 가리키고 있는 노드들(후순위에 있는 점들)
nodes = [[] for _ in range(n + 1)]
# 노드들의 진입차수
cnt = [0] * (n + 1)
# 후순위 노드들을 담고, 진입차수를 늘려준다.
for route in routes:
a, b = route
nodes[a].append(b)
cnt[b] += 1
# 스택 이용/ 진입차수가 0인 것들 부터
# stack = [1, 4, 6]
stack = deque([])
for i in range(1, len(cnt)):
if cnt[i] == 0:
stack.append(int(i))
answer = []
while stack:
target = stack.pop()
answer.append(target)
for node in nodes[target]:
cnt[node] -= 1
if cnt[node] == 0:
stack.append(node)
for i in range(len(answer)):
print(answer[i], end=' ')
#answer = [6, 5, 4, 1, 2, 3]이 경우 단순히 두 사람씩 키를 비교한 데이터만을 가지고 모두의 키가 오름 혹은 내림차순이 될 수 있도록 정렬해주고 있다. 여전히 주어진 데이터에 따라 여러가지 답이 존재 할 수 있다.
'sw사관학교 정글 2기 > 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘 (0) | 2021.08.30 |
|---|---|
| 다이나믹 프로그래밍 (0) | 2021.08.26 |
| 그래프 탐색 알고리즘: DFS/BFS (0) | 2021.08.19 |
| 정렬 (0) | 2021.08.11 |
| python 함수 정리 (0) | 2021.08.08 |



댓글